Содержание:
Одной из важнейших задач молочной промышленности всегда был учет объема продукта: поступившего на обработку, расходуемого в течение технологического процесса, полученного на выходе. Причем эти измерения требуются как для технологических задач, так и для экономического учета.
О современных способах произведения этих измерений и пойдет речь.Существует несколько подходов к измерению объема жидкости, находящейся в емкости. Все они, однако, имеют одну общую исходную величину, требуемую для расчета. Эта величина – высота столба жидкости.Известна формула, устанавливающая математическую связь между плотностью жидкости, высотой ее столба относительно точки измерения, ускорением свободного падения и давлением, оказываемым на дно и стенки сосуда:
где Р – давление, ρ – плотность жидкости, h – высота столба жидкости, g – ускорение свободного падения (9,8 м/c2).
Итак, зная давление и плотность жидкости, нетрудно рассчитать высоту, до которой она доходит относительно точки измерения. Такой способ измерения называется гидростатическим.Для того, чтобы узнать давление жидкости используются соответствующие датчики. В пищевой промышленности, как правило, это датчики с мембраной, имеющие относительно большую плоскость контакта со средой, что позволяет легко отмывать их от остатков продукта.
Среди датчиков давления наиболее распространены датчики с выходным сигналом 4…20 мА, являющимся общемировым стандартом в системах автоматического управления. Например, интеллектуальный датчик давления 4000-SAN.Сам чувствительный элемент датчика обычно представляет собой тензорезистор – элемент, изменяющий свое сопротивление в зависимости от приложенного к нему усилия. Зависимость сопротивления этих элементов от давления известна. Далее изменение сопротивления электроника датчика приводит к сигналу 4…20 мА.Современные датчики давления часто делаются цифровыми – то есть роль преобразователя играет микроконтроллер, встроенный в датчик. Такие датчики легче настраивать, они обладают более высокой точностью и могут оснащаться дисплеями, модулями коммуникации и дополнительными функциональными возможностями.
Итак, после того, как получено значение высоты, можно переходить к расчету объема жидкости. Выделяются два основных практических подхода:
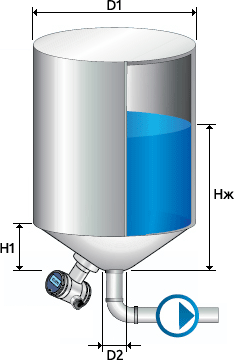
Первый способ подразумевает возможность выражения зависимости высота – объем известной формулой. Он актуален для емкостей, имеющих несложную форму и построенных из таких стандартных геометрических фигур, как, например, полусфера, конус и цилиндр. Например, для широко распространенных емкостей в форме цилиндра с коническим дном (Рисунок 2), вычисление будет производиться следующим образом: до тех пор, пока жидкость не достигла края конуса зависимость ее объема от высоты такова:
Где V – объем, Нж – высота столба жидкости, K – конусность
как только высота жидкости достигает края конуса и начинает заполнять цилиндр достаточно взять заранее вычисленный полный объем конической части:
и прибавлять к нему объем жидкости, находящейся в цилиндрической части:
С учетом степени развития микроконтроллеров, подобный алгоритм возможно реализовать непосредственно в датчике. Не нужно никакое внешнее устройство – датчик сам вычислит объем жидкости, если ввести ее плотность и геометрию емкости.Этот способ, однако, имеет определенные недостатки и ограничения. Они будут рассмотрены далее.
Отдельно нужно отметить требования к точности измерения давления, производимого датчиком. Нетрудно посчитать, что общепромышленный датчик давления, имеющий погрешность в 0,5 % для емкости высотой в 3 метра даст ошибку измерения в:
Значение не кажется столь большим. Однако, если емкость при этом имеет диаметр, скажем, в 2 метра, погрешность вычисления объема составит:
или 47,1 литров.
Достаточно большое значение, с учетом того, что в течение рабочего дня могут производиться десятки циклов наполнения/опустошения емкости. При этом данное значение не учитывает дополнительную погрешность, вызываемую перепадами температуры.Именно поэтому датчики для решения задач вычисления объема обычно имеют погрешность не более 0,1 %. При тех же условиях, такой датчик даст ошибку измерения всего в 9,42 литра, то есть в 5 раз меньшую.
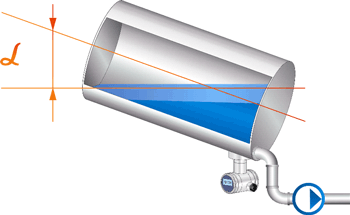
На практике часто встречаются емкости, имеющие искажения формы внутренней поверхности, к которым неприменим геометрический метод вычисления объема емкости.Например, для емкости, установленной под углом (Рисунок 2), наклон в 2…3 градуса, кажущийся незначительным, сильно нарушит точность измерений – в горизонтальной емкости поверхность жидкости вместо прямоугольника будет иметь гораздо более сложную форму, что значительно меняет зависимость объема от уровня.
Емкость может иметь утопленный в стенку люк. В этом случае нужно производить вычисления уже по трем разным формулам, вместо двух. К тому же, зависимость объема на участке с люком будет куда более сложной, чем для прямого цилиндра. Также, геометрический метод на практике неприменим к емкостям, в которых производится перемешивание продукта.
Массивное устройство внутри емкости значительно исказит результаты вычислений – датчик будет показывать объем, больший, чем реальный. Предусмотреть готовые алгоритмы для каждой подобной ситуации и внести их в датчик – задача практически невыполнимая. Тут на помощь приходит более трудоемкий, но и значительно более гибкий способ измерения. Если начать заливать в емкость, допустим, по 100 литров жидкости и при этом на каждом шаге отмечать высоту, соответствующую залитому объему, мы получим так называемую «тарировочную таблицу». Суть в следующем: нестандартная форма емкости моделируется с использованием некоторого количества прямых отрезков. Чем их больше, тем точнее будут производиться вычисления. Таким образом, можно высоте столба жидкости поставить в соответствие ее объем.
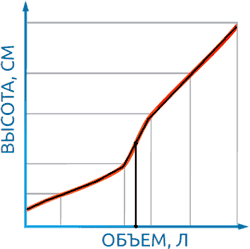
Если жидкость, например, находится посередине между двумя точками, то и объем вычисляется, как среднее значение объемов в этих точках (Рисунок 3). Очевидно, что от количества точек, используемых при тарировании, значительно зависит точность результата. Если для участка с линейной зависимостью объем/высота достаточно двух точек, до для нелинейных участков их требуется гораздо больше. Тарирование на нелинейном участке можно производить шагами, в два раза большими, чем допустимая погрешность на данном участке. Например, если в конусной части емкости необходимо получить точность не ниже 20 литров, шаги тарирования должны быть не более 40 литров. Тут следует помнить простое правило – чем меньше шаги и больше точек, тем выше итоговая точность работы. Недостаток метода в том, что датчик, перенесенный на другую емкость, снова потребует тарирования. Однако, единожды оттарированный на одной емкости датчик будет не только давать максимально высокую точность вычислений, но и позволит подсчитывать объем для жидкостей с различными плотностями – достаточно будет лишь ввести в него это значение.
Это значит, что можно произвести тарирование с использованием обычной воды, а затем, предварительно поменяв значение плотности жидкости в памяти датчика, заливать продукт, имеющий плотность, отличную от плотности воды. Таким образом, мы получаем гибкий и точный метод, позволяющий работать с емкостями любой формы и жидкостями любой плотности.
Инженер отдела проектирования ООО «КИП-Сервис»
Горбоносов М.А.
При добавлении товара возникла ошибка. Пожалуйста, повторите попытку чуть позже.